

|
| Home | Research | Publications | Recent news | Group | Teaching |
|
Occupation matrix control in VASPSelf interaction and density functional theory + UThe self-interaction error (SIE) that is inherent in density functional theory (DFT) is a well-known problem for electronic structure calculations. The SIE arises through the approximations used to determine the exchange and correlation. These approximations result in the exchange not cancelling the self-Coulomb term, which causes an electron to effectively see itself. The result is an erroneous repulsion which artificially favours electron delocalisation and is especially problematic for d- and f-element systems which possess strongly localised electrons. Both on-site correction terms and hybrid functionals (which mix in a portion of exact exchange) have been widely used to correct for the SIE. DFT+U, where U is a Hubbard-type correction that penalises against delocalisation, is a popular methodology used in computational materials chemistry, representing a good trade-off between accuracy and computational efficiency. The equation for the Dudarev version of this approach is: 
where The results of this can be seen in the simulation of reduced cerium dioxide shown below. On removal of an oxygen atom two electrons are left behind. In the case of the standard DFT these two electrons incorrectly delocalise due to the SIE while once a +U correction is applied (U=5 in this case) the expected localisation is achieved. 

Occupation matrix controlWe have implemented occupation matrix control within the VASP simulation code. This works by controlling the orbital occupation in the DFT+U calculation through occupation matrices. For a d-atom, the orbital occupation can be set through the use of two occupation matrices, one for up spin and the other down spin. For each matrix, assuming the setting of an integer occupation along each element of the leading diagonal, from d-2 in the top left hand corner to d2 in the bottom right corner. This gives rise to full occupation of the specified orbital within the x,y and z axes defined in the simulation cell. To adjust the shape or to rotate the orbital, off-diagonal elements in the matrix can be set. The occupation matrices are diagonalised to obtain an orthogonal set of orbitals and occupations. This occupation matrix control therefore only acts to influence the specified occupation, as it does not directly alter the charge density or wavefunction information. However, tests have indicated that this approach is typically sufficient to obtain a specified orbital occupation. From a procedural point of view, the simulations are first minimised with the occupation matrix control method. The control is kept on until the ionic and electronic structure have fully minimised, thus creating any structural distortion that may arise based on the specified occupation (polaron). The energy from this run however is meaningless, due to their artificial manipulation of the DFT+U calculation. Therefore, the structure is then further minimised from the distorted structure and wavefunction information, but with no occupation matrix control applied. This allows an appropriate energy to be obtained and allows for any orbital distortion/rotation away from the idealised fully ionic case. Any orbital configurations which have a sufficiently low barrier can then minimise to an alternative, more stable configuration. However, if there is a significant barrier then the optimisation of the electronic structure may be restricted to the local minimum thus giving rise the a metastable state. Finally, if necessary, the simulation can be further minimised with the structural data alone and the wavefunction information removed. This potentially allows any further distortion away from a metastable state to be achieved. Furthermore, it also allows the methodology to be assessed for its role as a tool for directing localisation to a particular lattice site. Application to a tetrahedral [TiF4]-1 clusterAs a test of the approach, a single metal centre cluster was used to assess the ability of the occupation matrix control to direct the electron occupation. To achieve this for d orbitals,` a cluster of [TiF4]-1 was set up so that the x, y and z axes of the cell correspond to the normal definition. By applying occupation matrix control an integer occupation of each of the orbitals (with occupation set to one on the leading diagonal matrix) was investigated within a tetrahedral symmetry. Occupation of each of the orbitals was obtained through the occupation matrix control and when turned off the orbital occupation remains. The figure below shows the occupation of each of the orbitals and the associated energies showing the expected splitting pattern with two distinct orbital sets observed. The e set (comprised of d0 and d2) lowest in energy, with d-2, d-1, and d1 forming the t2 set 0.41 eV above. 




The cluster was also simulated with no occupation matrix control and in this case the calculation find one of the low energy set. 
Application to a tetrahedral [CeF4]-1 clusterApplication to a tetrahedral Ce(III) cluster was used to examine f orbital control. Initial tests examined the general set of f orbitals and which are defined by the integer occupation of the leading diagonal in the 7 x 7 occupation matrix. All general f orbital occupations were successfully achieved. The splitting pattern gives rise to one low energy orbital (f2), with a second slightly above this (f-2), a third level (f0) and 4 high energy orbitals (f-3, f-1, f1 and f3). 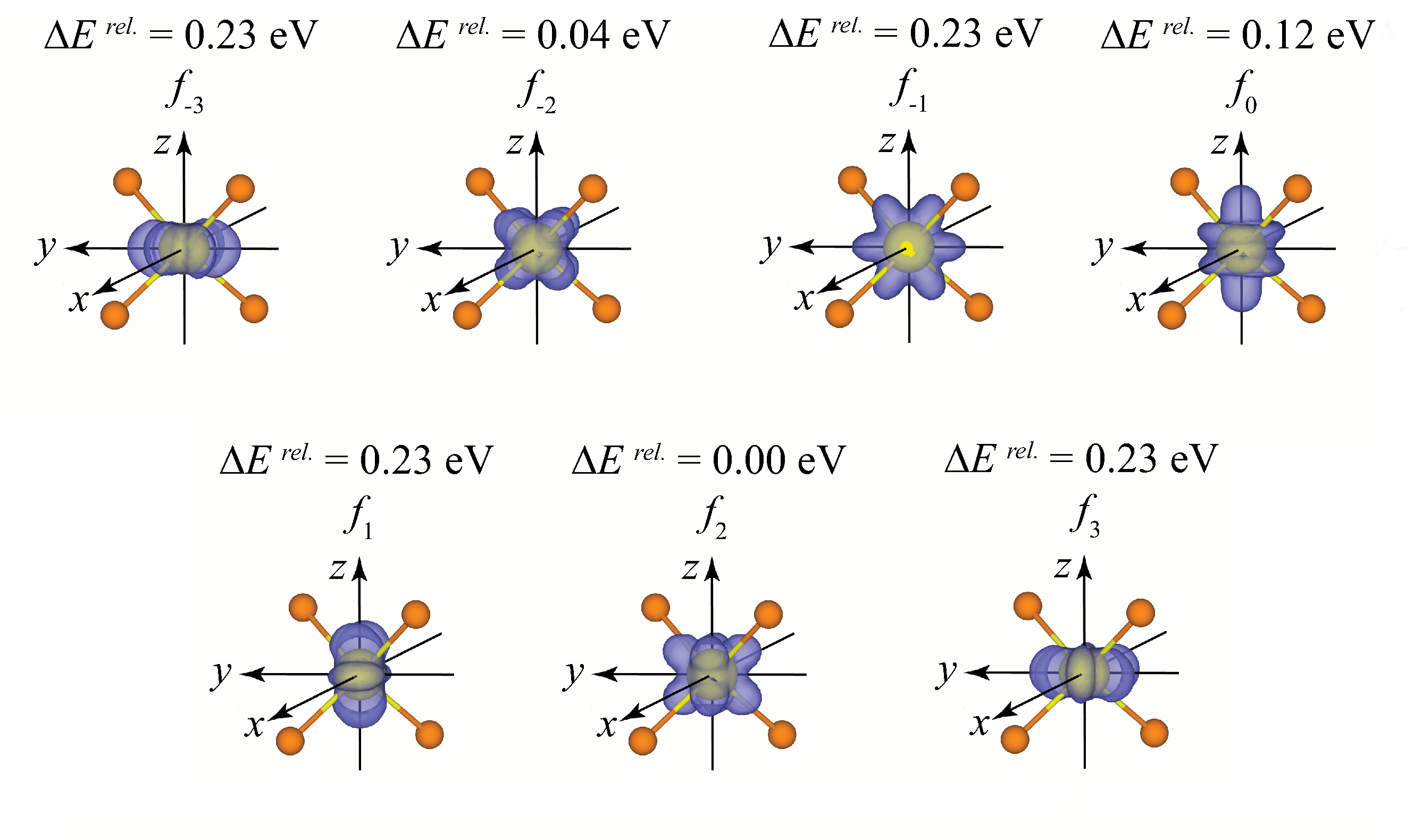
This not the expected splitting of two triply degenerate levels and a seventh single level (the order varies depending on the degree of covalent bonding). This occurs because the general set is not of the correct symmetry for the cubic field generated by the ligands in a tetrahedral arrangement. For this, linear combinations of the high energy f-3, f-1, f1 and f3 must by taken to generate a cubic set of orbitals. 
The cubic occupation are specified using the the leading diagonal for the specified orbitals and the off diagonal elements to control the mixing. For example the f-3>-1 can be roughly specified as: 
Occupation of all the cubic orbitals was achieved giving rise to two sets of two orbitals which are degenerate. If we combine these to the three remaining general orbitals we get the expected splitting patters with a triply degenerate set composed of f2, f-1>-3 and f1>3, a single orbital (f-2) and a triply degenerate set made up of f0, f-3>-1 and f3>1. 
With no occupation matrix control the simulation optimised into the f-2, which is not the ground state. The calculation fails to find one of the three low energy orbitals hence showing the problem of local minima on the potential energy surfaces when applying the DFT+U methodology, even to something as simple as a single metal centre cluster. 
Application to an oxygen vacancy in TiO2Will be added soon Access to occupation matrix code The occupation matrix control modifications were written by Prof. Graeme Watson. To enhance access to the code and encourage its free use, the occupation matrix control patch files for vasp will be available from the Watson group Git-Hub page VASPVASP (Vienna Ab-initio Simulation Package) is a software package created, distributed, and maintained by the Hafner Research Group at the University of Vienna. Related references:
Email: watsong AT tcd.ie Last updated: May 15 2014 Back to Top |